Logistic Regression
Overview
- Logistic regression vs. general linear regression
- Explanation of the math
- Testing effects & model fit
- Types of logistic regression
- Examples
Logistic
Regression vs.
General Linear Regression
How They Differ & What They Share
- Logistic regression is used when the outcome is
dichotomous
- Has / doesn’t have a disorder, recovers / dies, etc.
- General linear regression is used when the outcome is
continuous
- Or at least can be assumed to be so, even if we have only a few levels
- Both:
- Assume a linear relationship between predictors & outcome
- Assume error is normally distributed
- Can be used to test main effects, interactions (i.e., mediation), moderation, and model fits
So why use logistic regression?
The Problem of a Dichotomous Outcome
- Ma, He, & Ouyang (2022) investigated pneumonia deaths in ICUs from patients’ age, etc.
- Found (among other things¹):
| Predictor | β | OR | p |
|---|---|---|---|
| Age | -0.07 | -0.94 | .047 |
- I.e., as one ages, they become significantly less likely to survive pneumonia in an ICU
- Let’s predict survival by age…
- Including that high-quality nursing significantly improved one’s chances of survival (β = 1.01, OR = 2.72, p = .034).
Predicting Survival by Age
- The mean age of those who died was ~90 years
- SDs for age were roughly 4 years
- And β = -0.07
- So:
| Age | Predicted Survival |
|---|---|
| 82 | -0.14 |
| 86 | -0.07 |
| 90 | 0 |
| 94 | 0.07 |
| 98 | 0.14 |
| 150 | 1.05 |
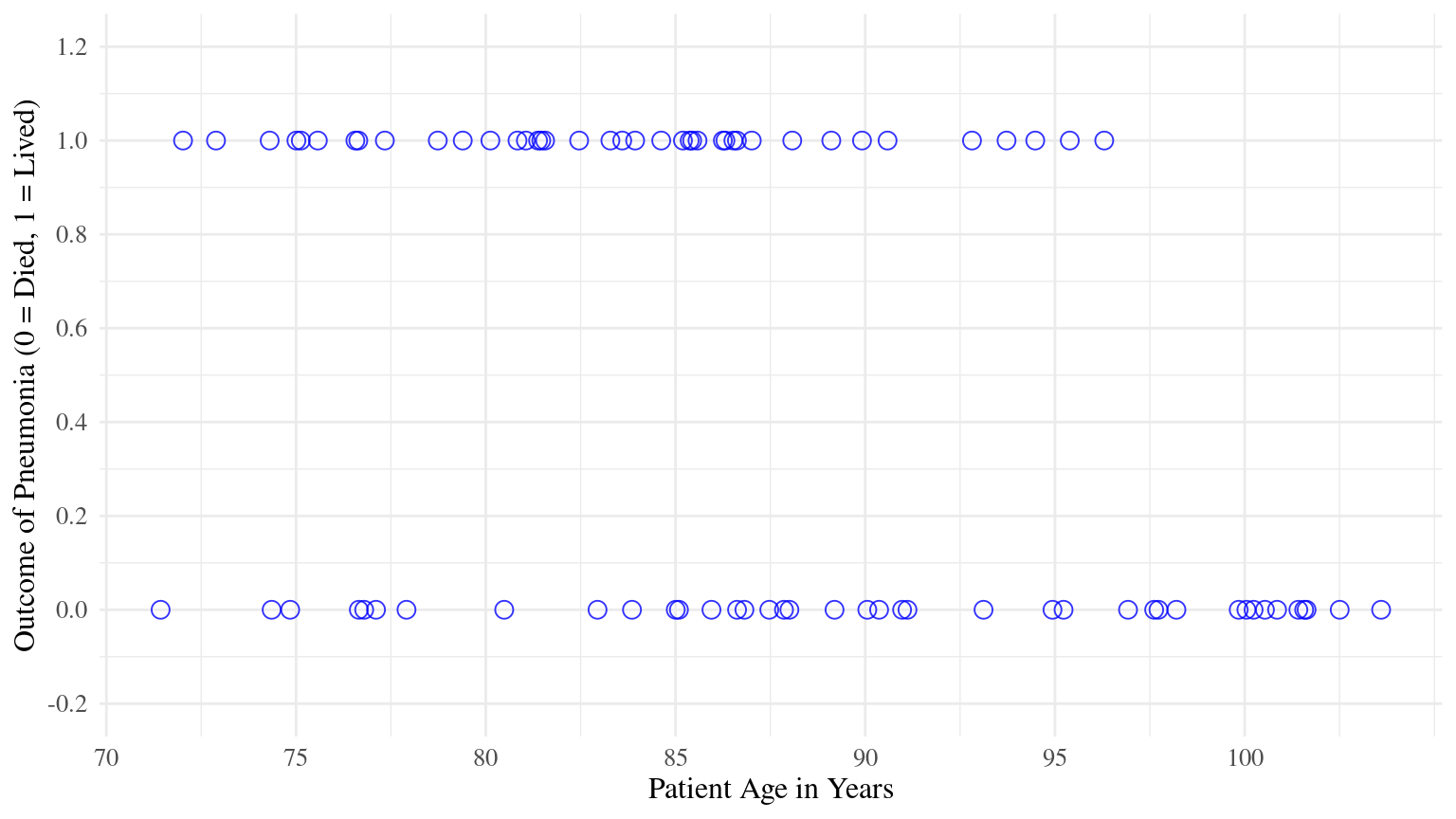
What the heck is a survival of -0.14? Or 1.05?
Dichotomous Variables Wholly Violate the Normality Assumption
library(ggplot2)
# Calculate mean values for Outcome = 0 and Outcome = 1
mean_outcome_0 <- mean(df$Age[df$Outcome == 0])
mean_outcome_1 <- mean(df$Age[df$Outcome == 1])
# Create the plot
plot <- ggplot(df, aes(x = Age, y = Outcome)) +
geom_point(size = 3, shape = 1, color = "blue", alpha = 0.8) +
scale_x_continuous(name = "Patient Age in Years", breaks = seq(80, 100, by = 5)) +
scale_y_continuous(name = "Outcome of Pneumonia (0 = Died, 1 = Lived)", breaks = seq(-0.2, 1.2, by = 0.2), limits = c(-0.2, 1.2)) +
theme_minimal(base_family = "serif") +
theme(
axis.title = element_text(face = "plain", size = 12), # Set face to "plain" for non-italic
axis.text = element_text(size = 10),
legend.position = "none"
)
ggsave("images/outcome_plot.svg", plot, width = 6, height = 5)
Plot of Simulated Data from Ma et al.
The Solution
- The solution to using linear regression for dichotomous data is … to not use dichotomous data
- Instead, we essentially transform the outcome into a probability
- “Essentially”
- As hinted at in Ma et al., we do this by first computing the odds of
a given outcome
- Based on the values of the predictors
- Thus using maximum likelihood to estimate the odds based on values of the predictors
- However, odds range from 0 to \(\infty\), so are very skewed
- The solution is to instead use the (natural)
logarithm of the odds
- Which ranges from \(\infty\) to \(\infty\)
Explanation of the
Math
Using Logs
We use odds instead of probabilities because the math is easier
But the odds themselves can be computed from the probabilities:
\[\text{Odds of Surviving} = \frac{P_{Surviving}}{1 - P_{Surviving}}\]We then take the natural log of that odds:
\[\text{ln}({\text{Odds}}) = \text{ln} \left( \frac{P_{Outcome}}{1 - P_{Outcome}} \right)\]This natural log of an odds is called a logit
- This logit is computed for every row in the data
- And is used instead of the dichotomous outcome
Actual Equation
- Therefore, the actual equation tested in logistic regression is:
\[\text{ln} \left( \frac{P_{Outcome}}{1 - P_{Outcome}} \right) = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} \ldots + \epsilon\]
- It follows the same form as other linear regressions
- It just transforms the outcome into a different value
Assumptios
- The assumptions
of logistic regression are the same as for other linear regression
models (using OLS or MLE):
- Observations are independent
- There is no severe multicollinearity among predictors
- Data and error are roughly normally distributed
- The relationship between each predictor and the logit of the outcome
is roughly linear
- (This assumption can be tested using the Box-Tidwell test)
- The sample size is sufficiently large
- As a rule of thumb, one should have at least 10 cases with the least frequent outcome for each predictor
Testing Effects
& Model Fit
Types of Tests
- As noted above, with logistic regression, we can test all of the things we can with general linear regression models
- However, the names are sometimes different
- Viz., we use the Wald χ² test instead of t-tests
- Otherwise, most tests use simple χ²
- And tests can be done on model fits (and changes in model fits)
- But testing information criteria
- -2 log likelihood and the modifications to it, e.g.:
- AIC (smaller penalty for mors complex models)
- BIC (larger penalty for more complex models)
- -2 log likelihood and the modifications to it, e.g.:
- But testing information criteria
Types of Logistic
Regression
Three Main Types of Logistic Regression
- Binary logistic regression
- The outcome is dichotomous
- Multinomial logistic regression
- The outcome can include three or more categories
- There is no natural ordering among the categories
- Ordinal logistic regression
- The outcome can belong to one of three or more categories
- And there is a natural ordering among the categories
Examples
Nursing Work Environment
& RNs’ Intentions to Leave

Choi, S. P.-P., Cheung, K., & Pang, S. M.-C. (2013). Attributes of nursing work environment as predictors of registered nurses’ job satisfaction and intention to leave. Journal of Nursing Management, 21(3), 429–439. doi: 10.1111/j.1365-2834.2012.01415.x
Satisfaction with Patient-Controlled Analgesia in Post-Op

Baek, W., Jang, Y., Park, C. G., & Moon, M. (2020). Factors influencing satisfaction with patient-controlled analgesia among postoperative patients using a generalized ordinal logistic regression model. Asian Nursing Research, 14(2), 73–81. doi: 10.1016/j.anr.2020.03.001
PPE & Mental Health Among Nurses During Covid-19 Pandemic

Arnetz, J. E., Goetz, C. M., Sudan, S., Arble, E., Janisse, J., & Arnetz, B. B. (2020). Personal protective equipment and mental health symptoms among nurses during the COVID-19 pandemic. Journal of Occupational and Environmental Medicine, 62(11), 892–897. doi: 10.1097/JOM.0000000000001999