Association
&
Causation
Overview
- Individual Differences and Correlations
- Types of Correlation Statistics
- Partial and Semipartial Correlations
- Concerning Causality
Individual Differences and Correlations
The Nature of Variability
- We assume that people differ (or might differ) with respect to their
behaviors, genetics, attitudes/beliefs, etc.
- Inter-individual differences: differences between people (e.g., in their levels of an attribute)
- Intra-individual differences: differences emerging in one person over time or in difference circumstances (e.g., change)
Importance of Individual Differences
- For health & social science research:
- We seek to understand differences among people (causes, consequences, etc.)
- For applied health & social science science:
- Important decisions/interventions are based upon differences among people
Variability and Distributions of Scores
- A set of test scores (from different people) is a “distribution” of scores.
- The differences within that distribution are called “variability”
- How can we quantitatively describe a distribution of scores,
including its variability?
- At least three kinds of information
- Central tendency
- Variability
- Shape (e.g., skew, kurtosis, normality)
- At least three kinds of information
Example of Describing a Distribution
- A set of systolic blood pressure (SBP) measurements:
| SBP |
|---|
| 118 |
| 126 |
| 132 |
| 110 |
| 144 |
| 120 |
Describing a Distribution:
Central Tendency
- What is the typical score in the distribution?
\(\mathsf{{Mean} = \overline{X} = \frac{\Sigma X_{i}}{N}}\)
\(\mathsf{\overline{X} = \frac{118 + 126 + 132 + 110 + 144 + 120}{6} = \frac{750}{6} = 125}\)
| SBP |
|---|
| 118 |
| 126 |
| 132 |
| 110 |
| 140 |
| 120 |
Describing a Distribution:
Variability
- To what degree do the scores differ from each other?
- Described as either:
- Variance
- The degree to which scores deviate (differ) from the mean
- Designed to accentuate larger distances
- Variance
\[\mathsf{{Variance} = s^{2} = \frac{\Sigma{(X_{i} - \overline{X})^2}}{n-1}}\]
Describing a Distribution:
Variability (cont.)
- Or—more often in manuscripts—as:
-
Standard deviation
- How far, on average, individual scores deviate from the sample mean
- Computed directly from variance
-
Standard deviation
\[\mathsf{{SD} = s = \sqrt{Variance}}\]
Describing a Distribution:
Variability (cont.)
\(\mathsf{s^2 = \frac{(X_{1} - \overline{X})^2 + (X_{2} - \overline{X})^2 + (X_{3} - \overline{X})^2 + (X_{4} - \overline{X})^2 + (X_{5} - \overline{X})^2 + (X_{6} - \overline{X})^2}{N - 1}}\)
\(\ \ \ \ \mathsf{= \frac{(118 - 125)^2 + (126 - 125)^2 + (132 - 125)^2 + (110 - 125)^2 + (144 - 125)^2 + (120 - 125)^2}{6 - 1}}\)
\(\ \ \ \ \mathsf{= \frac{(-7)^2 + (1)^2 + (7)^2 + (-15)^2 + (19)^2 + (-5)^2}{5}}\)
\(\ \ \ \ \mathsf{= \frac{49 + 1 + 49 + 225 + 361 + 25}{5}}\)
\(\ \ \ \ \mathsf{= \frac{710}{5}}\)
\(\ \ \ \ \mathsf{= 142}\)
| SBP |
|---|
| 118 |
| 126 |
| 132 |
| 110 |
| 140 |
| 120 |
Describing a Distribution:
Standard Deviation
\[\mathsf{Standard\ Deviation = \sqrt{Variance} = \sqrt{\frac{\Sigma(X_{i} - \overline{X})^{2}}{N - 1}}}\]
\[\mathsf{s = \sqrt{s^{2}} = \sqrt{142} = 11.92}\]
- On average, individuals’ scores were 11.92 units (mmHg) from the mean
Association Between Distributions
- Covariability: The degree to which two distributions of scores (e.g., X and Y) vary in a corresponding manner
- Two types of information about covariability:
- Direction: positive/direct or negative/inverse
- Magnitude: strength of association
Association Between
Distributions:
Covariance
- Covariance (Cxy): a statistical index of covariability
- Direction of association
- Positive association: Cxy > 0
- High scores on X tend to go with high scores on Y
- And low scores on X tend to go with low scores on Y
- Negative association: Cxy < 0
- High scores on X tend to go with low scores on Y
- And low scores on X tend to go with high scores on Y
- No association: Cxy = 0
- High scores on X tend to go with high scores on Y just as often as they go with low scores on Y
- Positive association: Cxy > 0
Association Between
Distributions:
Covariance
- But covariance does not provide clear information about the
magnitude of association
- Since its units of measurement are hard to interpret
- Measuring the covariance between BMI and blood pressure in what units? This?—
- Since its units of measurement are hard to interpret
\[\mathsf{\left( \frac{\text{kg} / \text{m}^{2}}{\text{mmHg}} \right)^{2}}\]
Association Between
Distributions:
Correlation
- Correlation (e.g., rxy, or just r): a standardized index of covariability
- Direction of association is the same as Cxy
- r > 0 Positive association
- r < 0 Negative association
- r = 0 No association
- Magnitude of association
- -1 ≤ r ≤ 1
- Stronger association as
r gets closer to ±1

Types of Correlation Statistics
Pearson Product-Moment Correlation
- The one you know about
- The correlation between two continuous (interval or ratio) variables
- Abbreviated as r
- The formula is also equal to the formula for a correlation between a
continuous variable & a dichotomous variable
- Called a point-biserial correlation
- Abbreviated rpb

Spearman’s rho (ρ)
- Spearman’s rank correlation (ρ)
- Summarizes correspondences between ranks
- Used for ordinal-ordinal comparisons
- And non-normal data
- Often, however, people use Pearson’s r assuming ordinal data is in fact interval
- Admittedly, the results are often similar to r
- But ρ is more robust than r
Kendall’s tau (τ)
- Used when data severely violate the assumptions of Pearson’s r, e.g., normality
- Its formula adjusts for non-normality:
\[\mathsf{\tau = \frac{(N_{\mathsf{Concordant\ Pairs}}) - (N_{Discordant\ Pairs})}{{Total\ Number\ of\ Pairs}}}\]
- But it’s inefficient:
- It does not use all of the available information
- And so may be less accurate
Partial and Semipartial Correlations

Partial Correlation
- A partial correlation allows us to see the correlation between two
variables …
- With a shared correlation (covariate) removed
- E.g., the correlation between BMI & blood pressure
- While removing the effect of age
- Or, e.g., the correlation between time to burnout
& nurse-to-patient ratio- While removing the effect of number of hours worked
Partial Correlation (cont.)
Formula (for Pearson’s r) is:
\[ \mathsf{r_{Y,X_1 \cdot X_2} = \frac{r_{Y,X_1} - r_{Y,X_2} r_{X_1,X_2}}{\sqrt{(1 - r_{Y,X_2}^2) \times (1 - r_{X_1,X_2}^2)}}} \]
E.g., the partial corr. between BMI & BP controlling for
Age:
\[ \mathsf{r_{BMI\ \&\ BP\ \cdot\ Age} = \frac{r_{BMI\ \&\ BP} - (r_{BMI\ \&\ Age} \times r_{BP\ \&\ Age})}{\sqrt{(1 - r_{BMI\ \&\ Age}^2) \times (1 - r_{BP\ \&\ Age}^2)}}} \]
Partial Correlation (cont.)

From: You, W., & Donnelly, F. (2023). Although in shortage, nursing workforce is still a significant contributor to life expectancy at birth. Public Health Nursing, 40(2), 229 – 242. doi: 10.1111/phn.13158
Partial Correlation (end)

Continued from You & Donnelly (2023)
Semipartial Correlation
- Also called a “part” correlation
- Removes the effect of a third variable from only
one of the two correlated variables
- Partial correlation removes the influence of X2 from both Y and X1
- Semipartial correlation removes the influence of
X2 only from X1
- E.g., the correlation between BMI & BP—removing only the effect of Age on BP
Semipartial Correlation (cont.)
- This is what, in fact, is done in linear regression
- We remove the effect of Predictor A on Predictor B
- (And vice versa)
- While still allowing Predictors A & B to each be associated with the outcome
- We remove the effect of Predictor A on Predictor B
Semipartial Correlation (cont.)
Formula semipartial correlation:
\[ \mathsf{sr_{Y,X_1 \cdot X_2} = \frac{r_{Y,X_1} - r_{Y,X_2} r_{X_1,X_2}}{\sqrt{1 - r_{X_1,X_2}^2}}} \]
Formula partial correlation:
\[ \mathsf{r_{Y,X_1 \cdot X_2} = \frac{r_{Y,X_1} - r_{Y,X_2} r_{X_1,X_2}}{\sqrt{(1 - r_{Y,X_2}^2) \times (1 - r_{X_1,X_2}^2)}}} \]
Semipartial Correlation (end)
E.g., semipartial corr. between BMI & BP, removing the effect of Age from BP:
\[ \mathsf{sr_{BMI\ \&\ BP\ \cdot\ Age} = \frac{r_{BMI\ \&\ BP} - (r_{BMI\ \&\ Age} \times r_{BP\ \&\ Age})}{\sqrt{1 - r_{BP\ \&\ Age}^2}}} \]
For partial it was:
\[ \mathsf{r_{BMI\ \&\ BP\ \cdot\ Age} = \frac{r_{BMI\ \&\ BP} - (r_{BMI\ \&\ Age} \times r_{BP\ \&\ Age})}{\sqrt{(1 - r_{BMI\ \&\ Age}^2) \times (1 - r_{BP\ \&\ Age}^2)}}} \]
Concerning Causality
The Problem of Causality
- Problem is proving that one thing caused an other
- Traditionally, viewed as nearly impossible to establish
- Requiring evidence for “counterfactuals”
- Proof of what would have happened in the same situation
- But with different influences
- I.e., saying X caused Y,
- Means Y would not have happened without X
- “I would have graduated from college
if I hadn’t burned out.”
- Proof of what would have happened in the same situation
The Problem of Causality (cont.)
- We get close to studying counterfactuals in science
- E.g.:
- Closely-matched participants in experimental designs (e.g., with controls)
- Longitudinal designs
- Especially following a “cohort” through time
- And alternating which undergoes what events
| Group | Time 1 | Time 2 |
|---|---|---|
| Cohort A | Treated | Nothing |
| Cohort B | Nothing | Treated |
The Problem of Causality (cont.)
- We get close to studying counterfactuals in science (cont.)
- E.g., mediated effects
- Comparing events without versus
with
considering some possibly-mediating effect
- Comparing events without versus
with
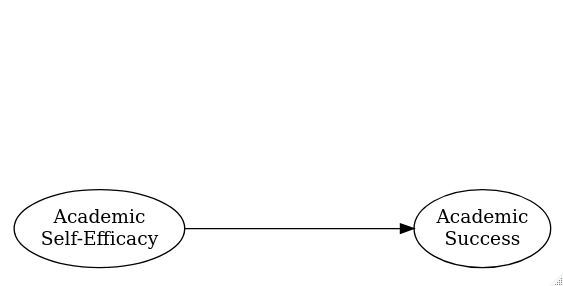
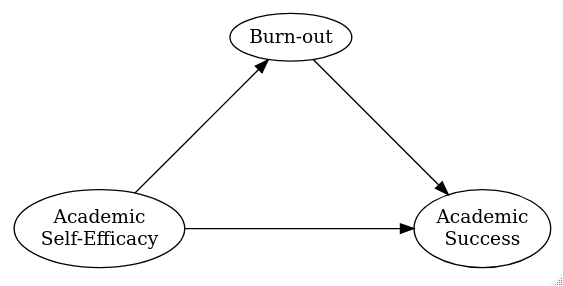
The Problem of Causality (cont.)


The Problem of Causality (cont.)
- Tests of mediated effects are currently considered among the best
measures of causality
- Since they are closest to being able to test a counterfactual
- But there is also a general trend
towards accepting causal
explanations in some areas
of research
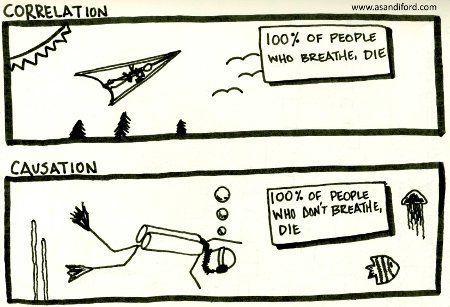
The Problem of Causality (end)
- E.g., Bulfone et al. (2022)
- Found that there is a direct effect of academic self-efficacy on academic success
- And that burn-out mediated part of that relationship
- (The effects were similar among TWIA males & females)

Causality without Counterfactuals
- Hill (1965)
proposed nine
guidelines to help evaluate whether an observed association may be
causal
- N.b., these are not strict rules
- “What I do not believe … is that we can usefully lay down some hard-and-fast rules of evidence [for] cause and effect.” (p. 299)
- N.b., these are not strict rules
- Offers a practical framework for causal reasoning
- Esp. where counterfactuals are difficult to study
- E.g., epidemiology, public & environmental health, policy analysis, etc.
- Esp. where counterfactuals are difficult to study
The End