Measuring
& Testing
Differences

Overview

  • Review of Assumptions in Inferential Statistics
  • Hypothesis Testing
  • Signal-to-Noise Ratio
  • Common Tests: t & F

Review of Assumptions in
Inferential Statistics

Assumptions in Inferential Statistics:
Representativeness

  • Three general types of assumptions:
  1. The sample represents the population
  2. That each data point (“datum”) is independent of the others
  3. That the population’s data are normally distributed
  • There are more/other assumptions that can be made, e.g.:
    • Other distribution shapes
    • Nature of any missing data
    • Whether data are continuous or discrete

Hypothesis Testing

Hypothesis Testing

Hypothesis Testing (cont.)

  • The “null” hypothesis is that there is no effect/difference
    • The p-value is technically the probability of finding the given pattern of data if the null is true
    • It’s couched this way mainly for philosophical reasons
      • I.e., that we can’t prove an effect,
        • But simply that there doesn’t seem to be
          nothing
      • Kind of like in criminal court
        • We don’t say that someone is “innocent,”
        • But that they are “not guilty”—that there
          isn’t enough evidence to prove guilt

Hypothesis Testing (cont.)

Hypothesis Testing (cont.)

Hypothesis Testing (cont.)

Hypothesis Testing (cont.)

Hypothesis Testing (cont.)

Hypothesis Testing (cont.)

Odds of Being Diagnosed with Various Comorbidities Among Older Adults with Opioid Use Disorders

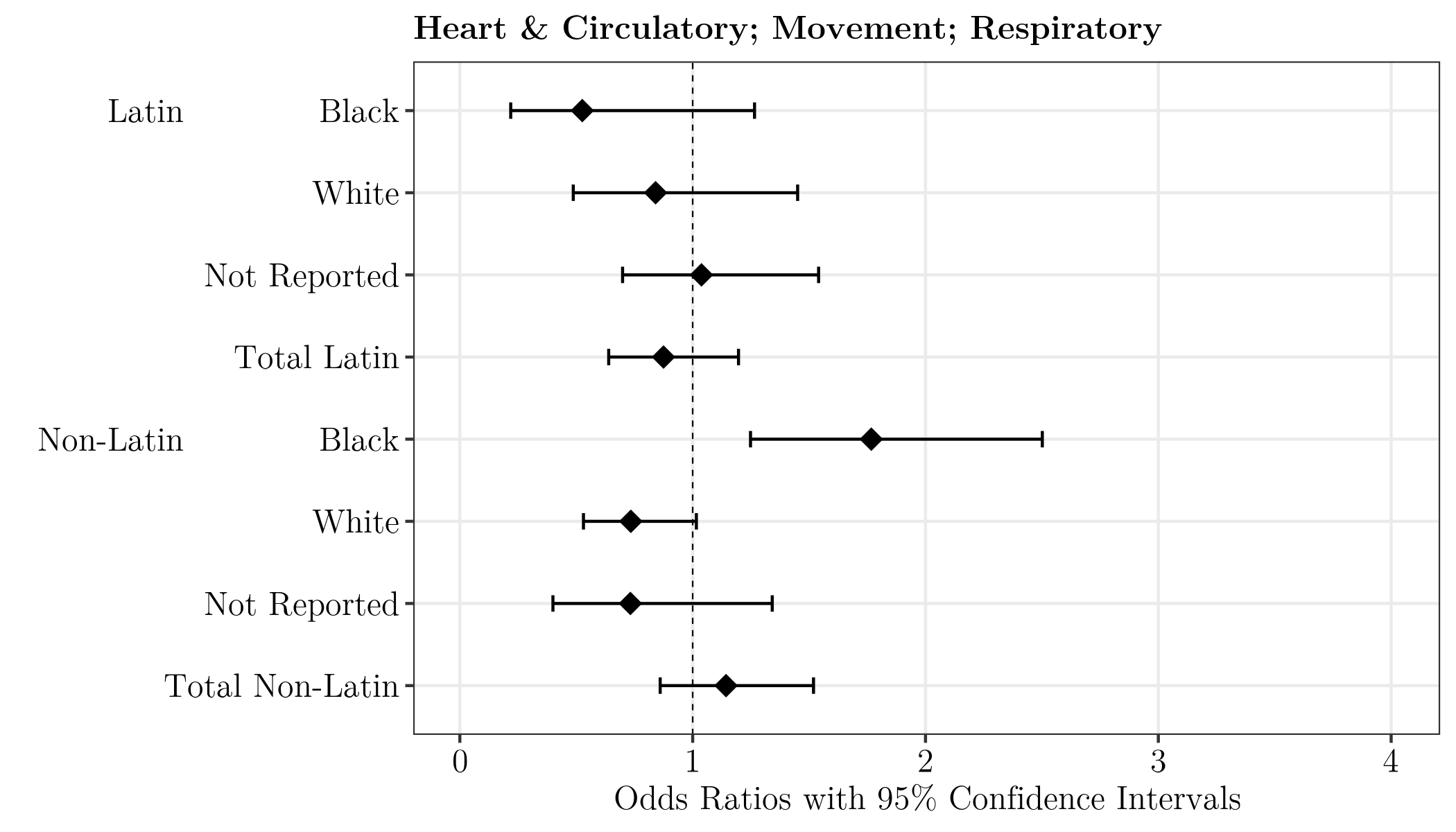
Baumann, S. & Samuels, W. E. (2024). Comparing comorbidities of older adults with opiate use disorder by race and ethnicity. Journal of Addictions Nursing, 34(12), 1280 – 1288. doi: 10.1097/JXX.0000000000000801.

Signal-to-Noise Ratio

  • Generally, information in a sample of data is placed into
    two categories:
    • “Signal,” e.g.:
      • Difference between group means,
      • Magnitude of change over time, or
      • Amount two variables co-vary/co-relate
    • “Noise”, e.g.,
      • Differences within a group
      • “Error”—anything not directly measured

Signal-to-Noise Ratio (cont.)

  • Many statistics & tests are these ratios
    • And investigating multiple signals & even multiple sources of noise
  • If there is more signal than noise,
    • Then we can test if there is enough of a signal to “matter”
    • I.e., be “significant”
  • E.g., the F-test in an ANOVA
    • A ratio of “mean square variance” between groups/levels vs. “mean square error” within each group
    • If F > 1, then use sample size to determine if the value is big enough to be significant

Signal-to-Noise Ratio (cont.)

Table 7.4: Tests of Between-Subject Effects on Health Literacy Knowledge

Source Sum of Squares df Mean Square F p Partial \(\eta^2\)
Information Intervention 4.991 1 4.991 5.077 .025 0.028
Telesimulation Intervention 0.349 1 0.349 0.355 .552 0.022
Error 172.061 175 0.983

  • \(\frac{\text{Signal}}{\text{Noise}}=\frac{\text{Mean Square Between}}{\text{Mean Square Error}}\)
  • E.g., for the Information Intervention: \(\frac{4.991}{0.983} = 5.077\)

Patton, S. (2022). Effects of telesimulation on the health literacy knowledge, confidence, and application of nursing students. Doctoral dissertation, The Graduate Center, CUNY.

Common Inferential
Tests: t & F

t and F Statistics

  • Very common tests of differences in means
    • These are signal-to-noise ratios
    • Cannot be significant if there is more noise than signal
      • I.e., if t < 1 or if F < 1
    • If >1, then can be significant if the sample is big enough
  • t is used to test the mean difference between two groups
    (“t for two”)
    • F is typically used for three or more groups
  • Mathematically:
    • The distributions of each strongly resemble
      normal distributions
    • t² = F

t-Tests

  • Also called Student’s t
  • Invented by William Gosset
    • Devised to test differences in small samples
  • Tests the size of a mean difference against a distribution of size differences one would expect if there was no real difference
    • I.e., if we got that mean difference just by chance

t-Tests (cont.)

  • The distribution tested against is a t-distribution
    • As the sample size increases, it approximates the normal distribution
    • Shape is determined by the degrees of freedom:
      • For small degrees of freedom,
        • It is more spread out and has heavier tails
      • For large degrees of freedom (df > 30 or so),
        • It closely resembles a normal distribution

Example of t-Tests

β-weights are tested via t- or F-tests.

Associations between:

  • Nurse staffing & skill mix and
  • Hospital consumer assessment of health care providers & systems (HCAHPS) measures
  • In pooled cross-sectional and longitudinal regression models

From Martsolf et al. (2016)

F-Tests

  • Invented by Ronald Fisher
    • Called “F” in his honor by George Snedecor, who used it in his contributions to creating ANOVA family tests
  • Devised to test signal-to-noise ratios
    • Thus seeing if enough variance is accounted for by a variable to be considered significant

F-Tests (cont.)

  • Turns out to be simply the square of a t-score (F = t2)
    • (And likewise tested against an F-distribution that also approximates a normal dist.)
  • Note that F-tests are relatively sensitive to deviations from normality
    • t-Tests are a bit
      less sensitive

Thank you