Intro
to
Linear Regression
Overview
- Review of Underlying Concepts in Inferential Statistics
- Understanding Linear Models
- An Example
- The Flexibility of Linear Models
- Further Considerations
Review of Underlying Concepts
Review of Underlying Concepts
- Variance & Covariance
- Importance in statistical analyses
- Covariance & Correlation
- Relationship between them
- Why use one or the other?
- Both are descriptive statistics
- Even though tests can be run on them
Review of Underlying Concepts (cont.)
- Assumptions made in computing correlations
- Measurement level is correctly conceived (ordinal, interval, ratio, etc.)
- Relationship is linear
- Assumptions made in testing their significance
- Monotonicity
- For Pearson’s r, also that variables are normally
distributed & homoscedastic
- And that the variables are bivariate normal
- For Pearson’s r, also that variables are normally
distributed & homoscedastic
- No big outliers
- Monotonicity
Review of Underlying Concepts (cont.)
- Partial & Semipartial Correlations
- Semipartial correlations remove the effect of another variable from one of the correlated pair
- Could remove the effect of several other variables from one of the
pair
- Which is conceptually the same thing we do in separating out the effects of various predictors on the same outcome
Review of Underlying Concepts (cont.)
- Correlations & Error
- Correlations separate dispersion into variance & covariance
- But make no assumptions about where error comes from
- However, when testing significance of Pearson’s r, error is assumed to be normally distributed
- Correlations separate dispersion into variance & covariance
Review of Underlying Concepts (end)
- Correlations & Error (cont.)
- The (unshared) variances of both variables comprise the denominator
- (This will be different for linear regression models)
- The (unshared) variances of both variables comprise the denominator
Understanding Linear Models
Buildling the Equation
- Simplest form of a linear relationship is \(Y = bX\)
- Where:
- \(Y\) = Outcome / response / criterion / DV
- \(X\) = Predictor / input / IV
- \(b\) = Slope of \(X\)
- The typical null hypothesis (H0) of “no effect” is
expressed here as:
\(b\) = 0
- The typical null hypothesis (H0) of “no effect” is
expressed here as:
- Where:
Buildling the Equation (cont.)
\[Y = bX\]
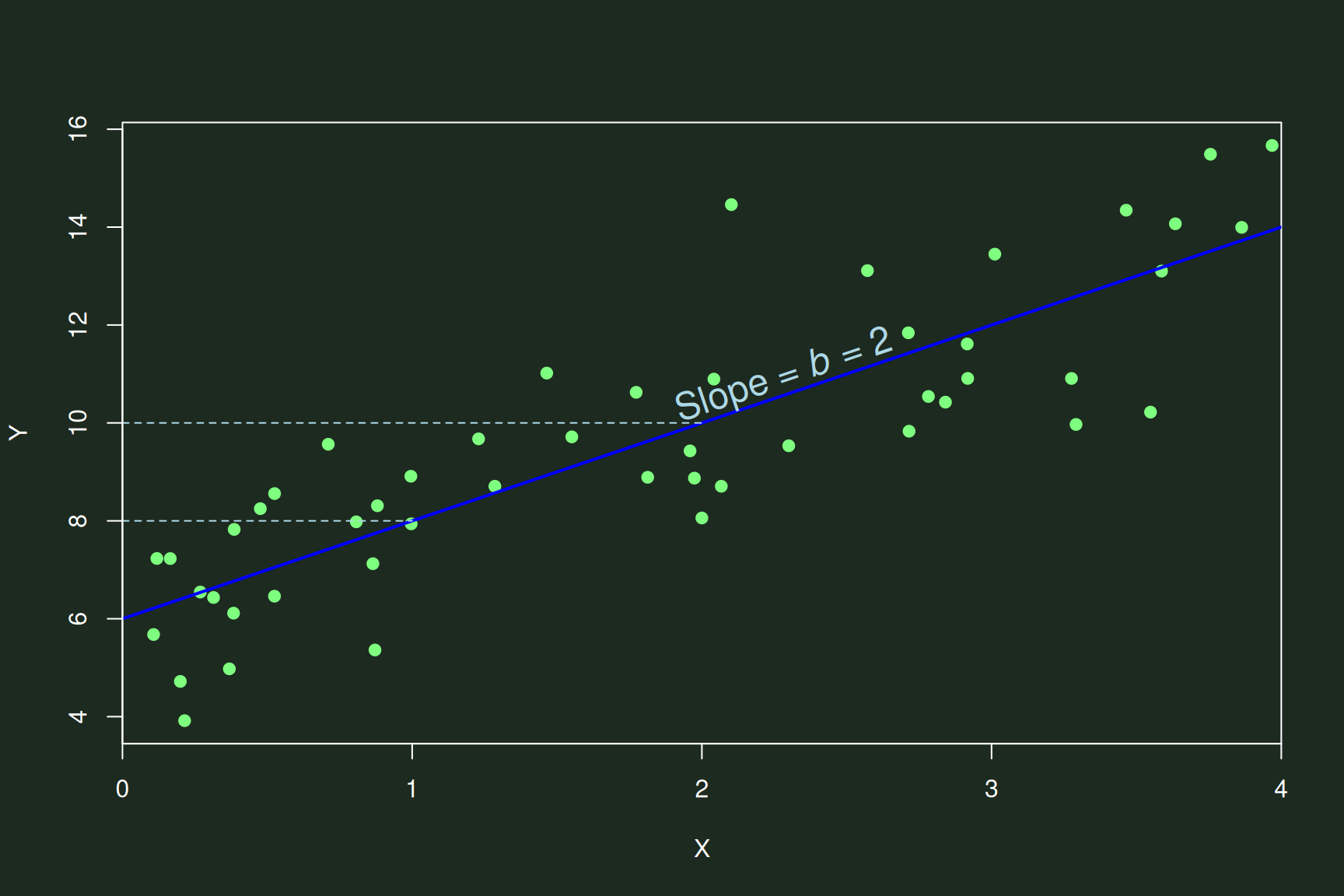
Buildling the Equation (cont.)
- However, we typically add more terms and notations to the equation
- The first term we add is the y-axis intercept
- And subscripts to differentiate it from the slope:
\(Y = b_{0} + b_{1}X_{1}\)- \(Y\) = Outcome
- \(b_{0}\) = Value of \(X_{1}\) at y-axis intercept
- \(b_{1}\) = Slope of \(X_{1}\)
- \(X_{1}\) = Predictor \(X_{1}\)
- And subscripts to differentiate it from the slope:
- The first term we add is the y-axis intercept
Buildling the Equation (cont.)
\[Y = b_{0} + b_{1}X_{1}\]
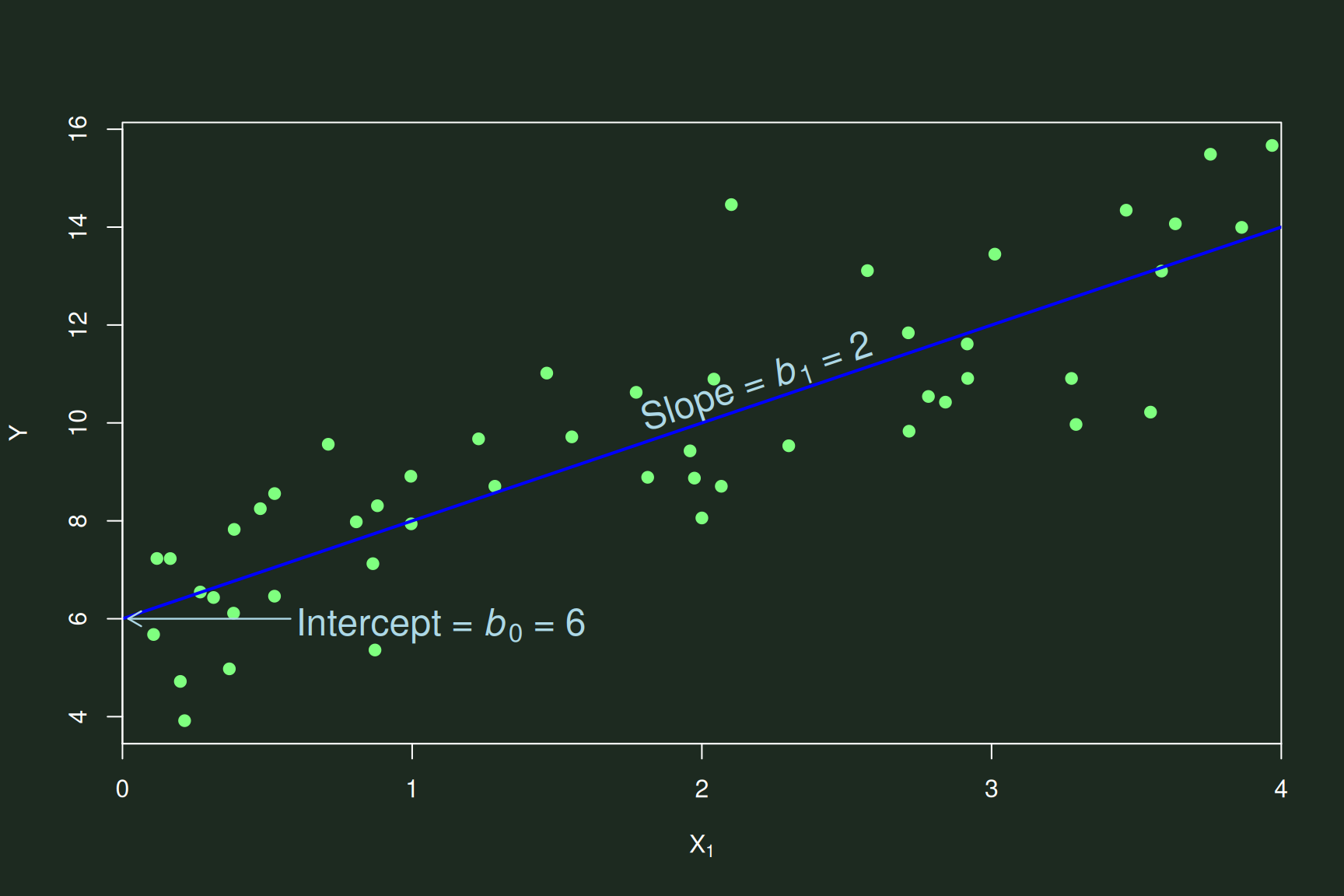
Buildling the Equation (cont.)
\[Y = b_{0} + b_{1}X_{1}\]
- We use the data to estimate:
- \(b_{0}\): The beginning/baseline value (when \(X_{1}\) = 0)
- \(b_{1}\): The effect of \(X_{1}\) on \(Y\)
- How much a (1-unit) change in \(X_{1}\) corresponds to a change in \(Y\)
Buildling the Equation (cont.)
- The equation so far is the model: \(Y = b_{0} + b_{1}X_{1}\)
- We are modeling a linear relationship between \(X_{1}\) and \(Y\)
- Assuming linearity, \(b_{0}\) & \(b_{1}\) contain all of the information about that \(X_{1}\)-\(Y\) relationship
- We can test the significance and effect size of the whole model
- How much of the relationship is accounted by that linear model
Buildling the Equation (cont.)
- But the model mis-estimates the actual data
- There is error in the model’s estimations
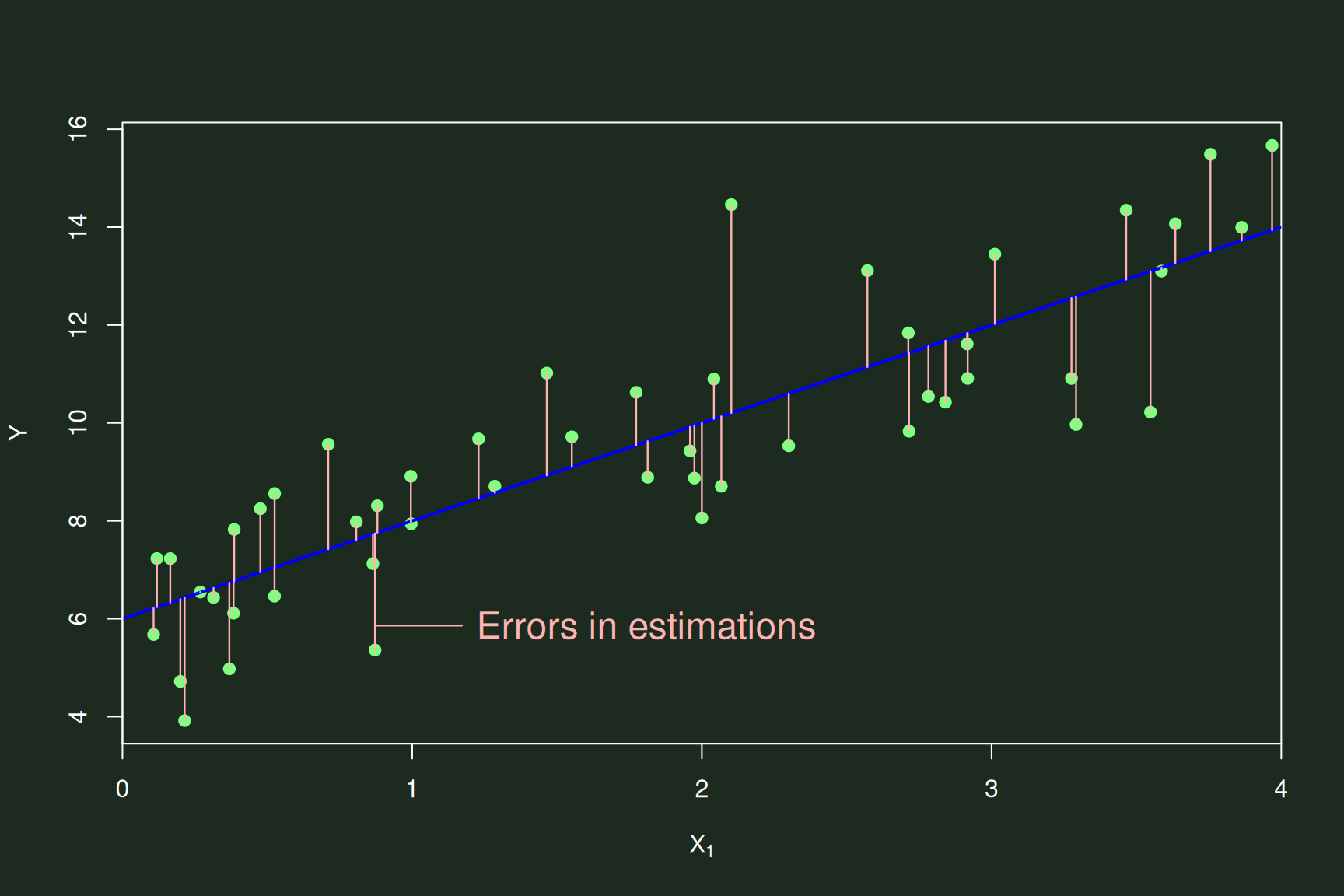
Buildling the Equation (end)
- We add this error to the equation:
\(Y = b_{0} + b_{1}X_{1} + e\)- \(Y\) = Outcome
- \(b_{0}\) = Value of \(X_{1}\) at y-axis intercept
- \(b_{1}\) = Slope of \(X_{1}\)
- \(X_{1}\) = Predictor \(X_{1}\)
- \(e\) = Error
- “Error” is thus information about the \(X_{1}\)–\(Y\) relationship not explained by the model
- But it is still the “noise” against which we test the model’s “signals” (\(b_{0}\) & \(b_{1}\))
More About the Equation
\[Y = b_{0} + b_{1}X_{1} + e\]
- Because error is separated out,
- The value of \(X_{1}\) is assumed to be measured without error
- Separating the intercept, slope, & error means each can be estimated & modified separately
- Note that Kim, Mallory, & Valerio (2022) present this equation as: \(y = a + b \times x + \sigma\)
More About the Equation (cont.)
- Adding more specificity to the equation:
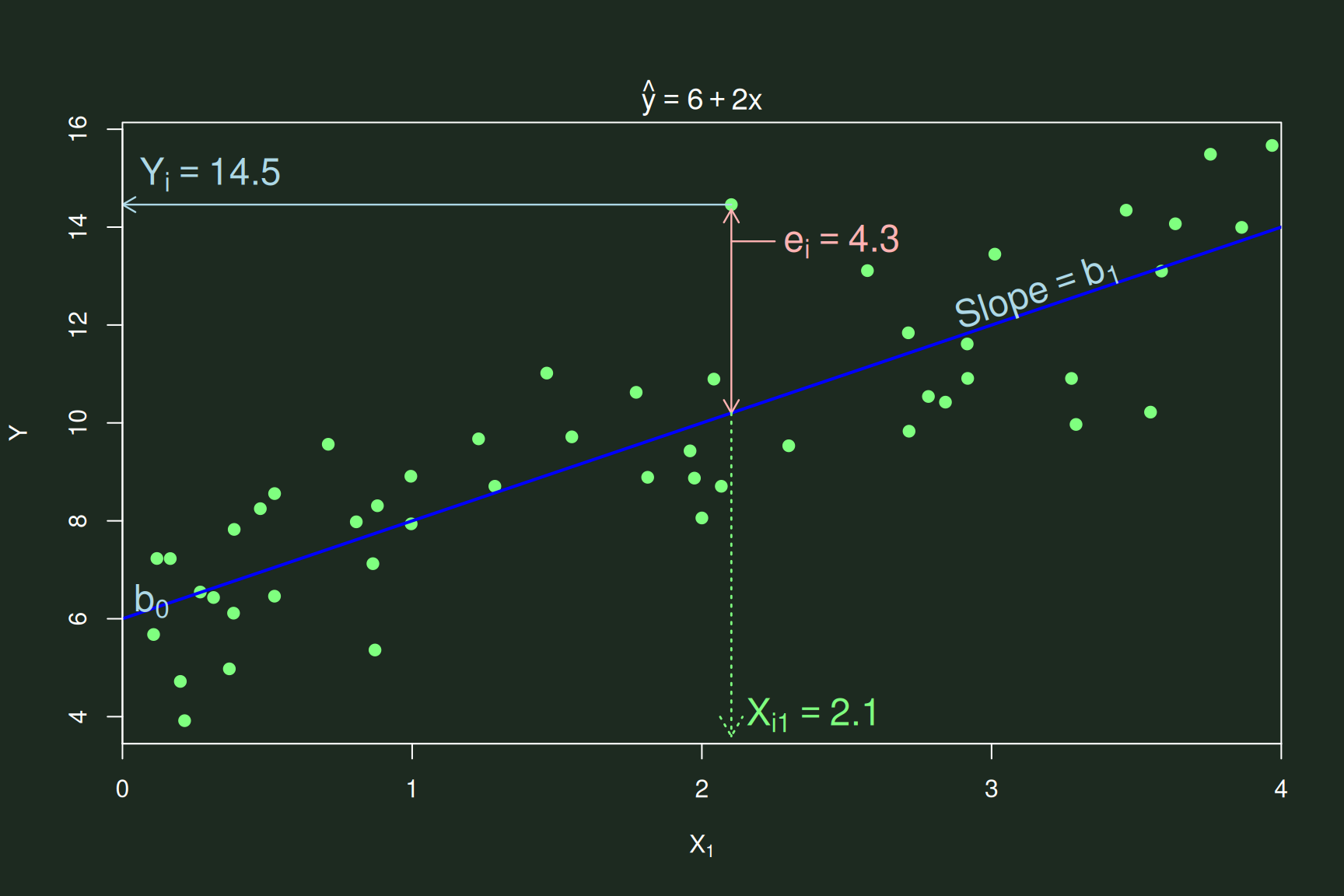
\(\hat{Y}_{i} = b_{0} + b_{1}X_{i1} + e_{i}\)- \(\hat{Y}_{i}\) = Predicted value of \(Y\) for participant \(i\)
- \(b_{1}\) = Slope for variable \(X_{1}\)
- \(X_{i1}\) = Value on \(X_{1}\) for participant \(i\)
- \(e_{i}\) = Error of measurement of participant \(i\)’s outcome
More About the Equation (end)
- Participant \(i\)’s score on \(X_{1}\) here is 2.1
- The predicted value of \(Y_{i}\) for participant \(i\) is:
- \(\hat{Y}_{i} = 6 + (2 \times 2.1) = 10.2\)
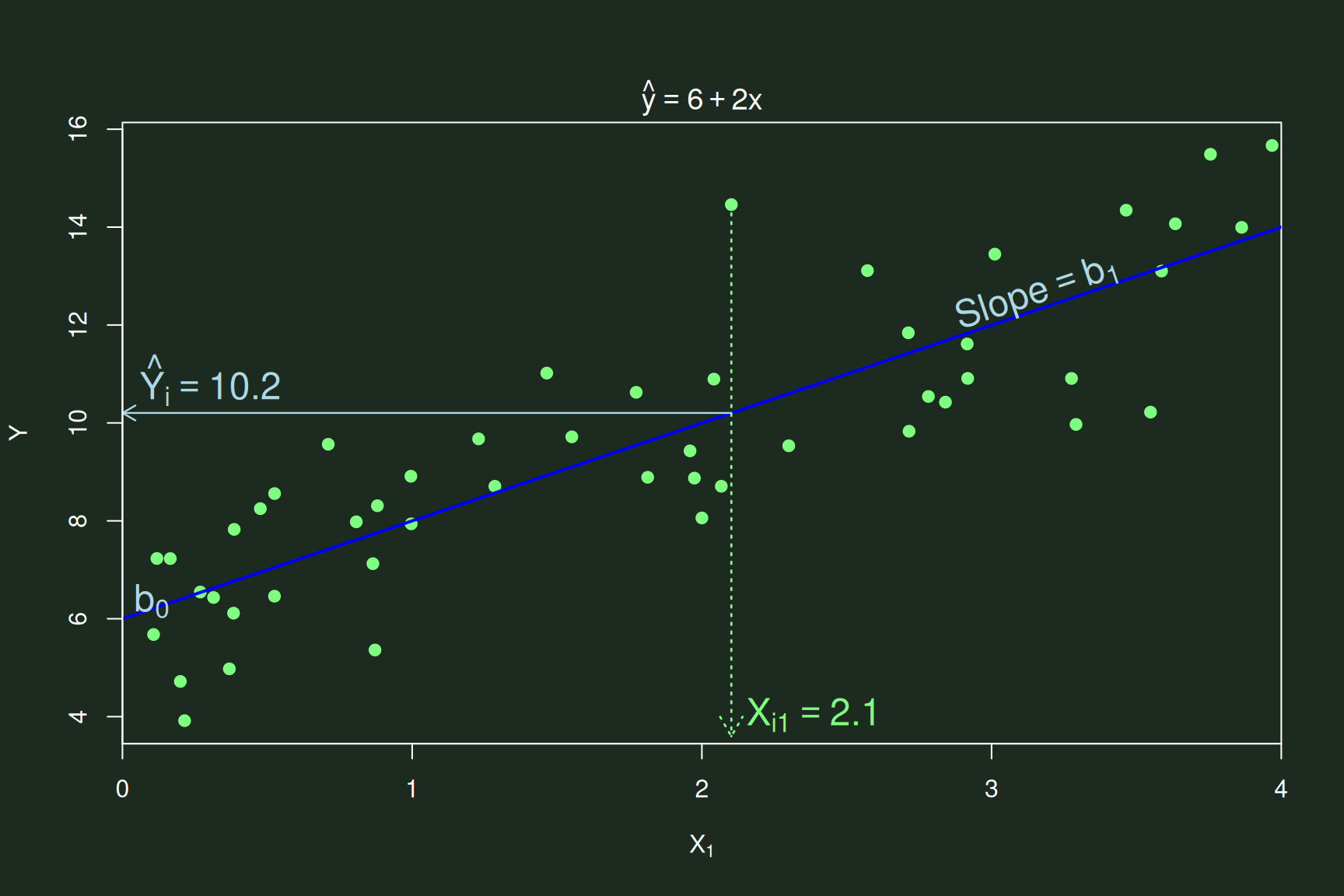
- The actual value of \(Y_{i}\) for participant \(i\) also includes the error:
- \({Y}_{i} = 6 + (2 \times 2.1) + 4.3 = 14.5\)
An Example
Predicting BMI from Sex & Neighborhood Safety
- Predicting body mass index levels among adolescents from:
- Whether an adolescent is biologically female
- Whether they feel their neighborhood is safe
- via SPSS (v. 29 & 31)
Data Used
- From the National Longitudinal Study of Adolescent to Adult Health
(Add Health)
- Using the prepared add_health.sav dataset
- Since data are longitudinal, only the first instance (wave) of data
collection was used
- Selected via:
Data>Select Cases...- Under
If condition is satisfied, addedWave = 1to select only the first wave
- Selected via:
Descriptives
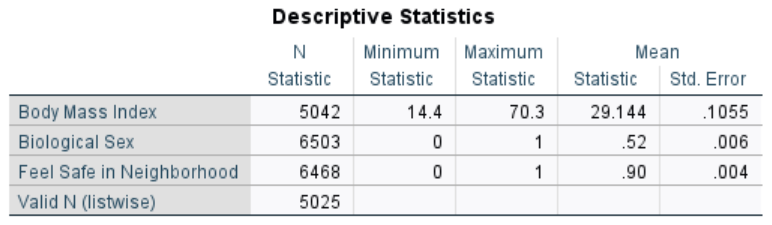
- The mean BMI (29.144) was obese (for adolescents)
- Since
Bio_Sexwas coded 0 =Male& 1 =Female, 52% of the participants were biologically female - And 90% reported feeling safe in their neighborhood
- About 77% (5025/6503) of cases had data on all three variables
Descriptives (cont.)
- BMI was positively skewed
- So, those with exceptionally high BMIs affect the results more
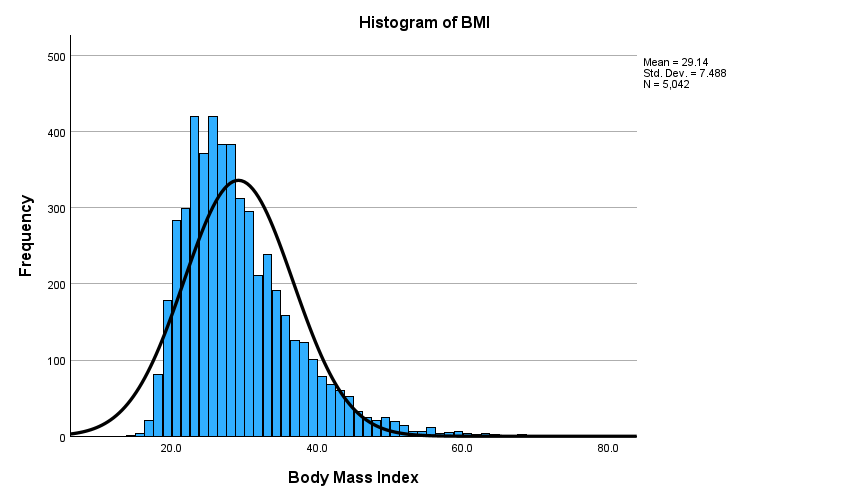
Descriptives: Q-Q Plot
Analyze>Explore...>Plots>Normality plots with tests- That skew—and a limited lower range—caused some deviations from normality
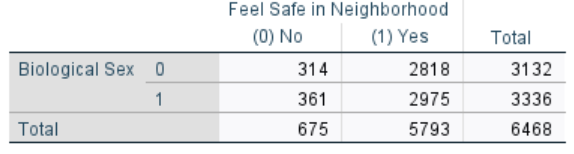
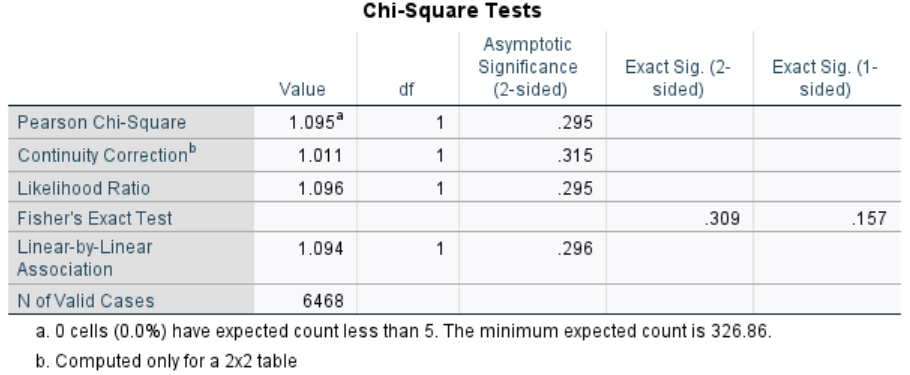
Descriptives: 2 × 2 Table
Analyze>Descriptives Statistics>Crosstabs...- The number of adolescents who felt safe in their neighborhood is not significantly different between the sexes
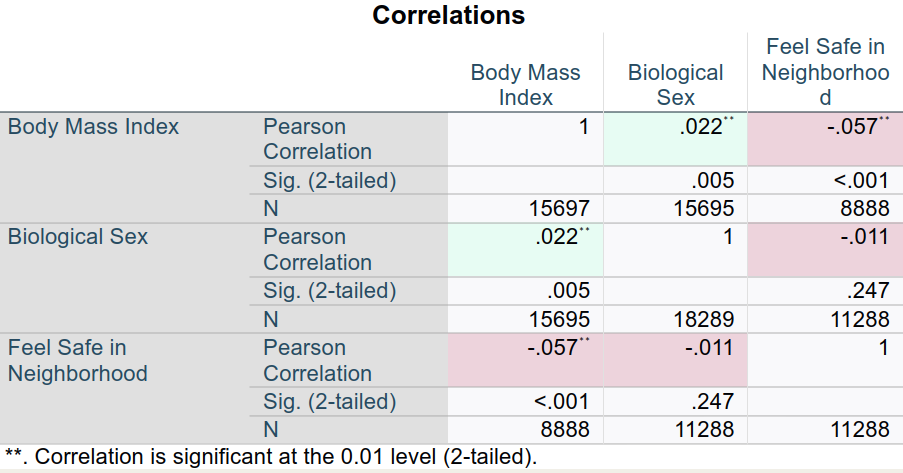
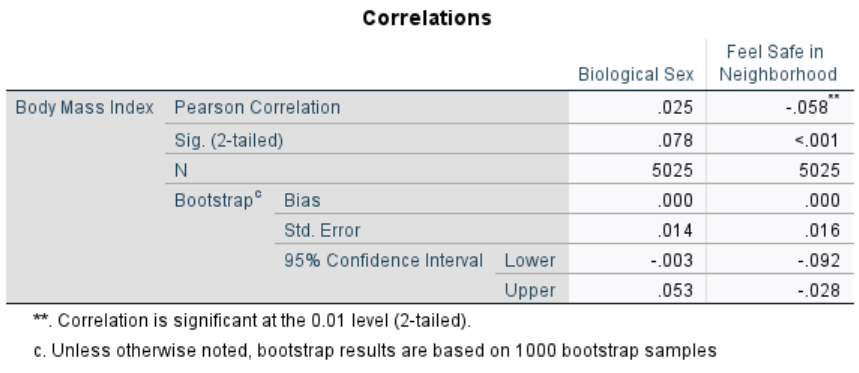
Correlations
- The correlations also reflect the weak relationship between
Bio_Sex&Feel_Safe_in_Nghbrhd - Feeling safe—but not sex—significantly correlated with BMI
Correlations with CIs
- The 95% confidence intervals (and correlations themselves) are slightly different when using Fisher’s r-to-z transformation versus bootstrapping
- Given the deviations from normality, bootstrapping is preferable here
95% confidence intervals generated from Fisher’s r-to-z transformation:
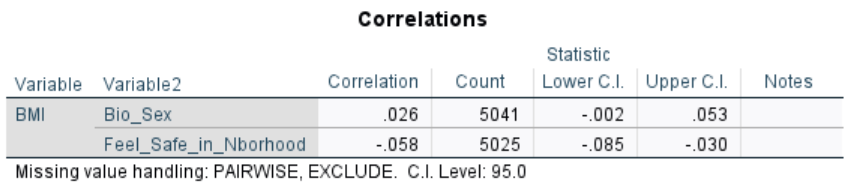
95% confidence intervals generated from bootstrapping:
Linear Regression
- Conducted via:
Analyze>Regression>LinearBMIasDependentBio_Sex&Feel_Safe_in_Nghbrhdas predictors inBlock 1 of 1
Linear Regression (cont.)
- The combination of
Bio_Sex&Feel_Safe_in_Nghbrhddid not explain much of the variance inBMIscores- The R² was .004; adjusted for number of terms in the model, it was .003
- This combination of variables thus only accounted for about 0.3% –
0.4% of the total variance in BMIs
- The high standard error, however, indicates that replications may find rather different R²s

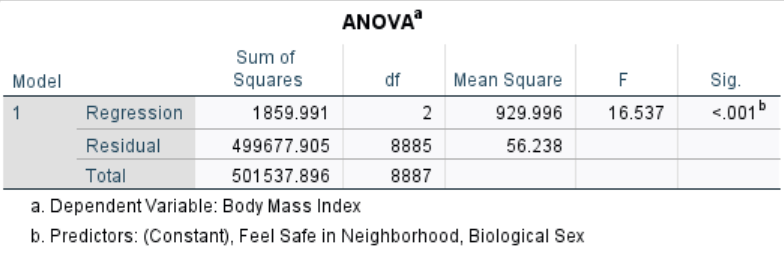
Linear Regression (cont.)
- Nonetheless, the model was significant
- The intercept & sample size both surely helped
- This ANOVA source table presents the effect of the overall model
- Like first testing a variable in an ANOVA before conducting post hocs, this helps protect against over-interpreting
Linear Regression (cont.)
- Biological sex & feeling safe in one’s neighborhood both significantly predicted BMI
- The standardized β for sex means its effect size was close to
“small”
- It is “medium” for feeling safe (q.v. η² criteria in this table)
- The positive effect for sex means those identifying as female (1s) tended to have higher BMIs than those identifying as male (0s)
- The negative value for feeling safe means those who felt safe (1s) tended to have lower BMIs than those who didn’t (0s)

Interpretting the Effects
- Writing these results in linear equation form:
\(\hat{\text{BMI}} = 30.205 + (0.325 \times \text{Sex}) + (-1.383 \times \text{Feeling Safe})\)

Interpretting the Effects (cont.)
\[\hat{\text{BMI}} = 30.205 + (0.325 \times \text{Sex}) + (-1.383 \times \text{Feeling Safe})\]
- Since
Bio_Sexwas coded 0 =Male& 1 =Female- And
Feel_Safe_in_Nghbrhdas 0 =No& 1 =Yes,
- And
- We predict that the BMI
- For a male (0)
- Who does not feel safe (0)
- Is 30.205:
\[\begin{align*} \hat{\text{BMI}} & = 30.205 + (0.325 \times 0) + (-1.383 \times 0) \\ & = 30.205 + 0 + 0 \\ & = 30.205 \end{align*}\]
Interpretting the Effects (cont.)
\[\hat{\text{BMI}} = 30.205 + (0.325 \times \text{Sex}) + (-1.383 \times \text{Feeling Safe})\]
- The predicted BMI for
- A female (1)
- Who does not feel safe (0)
- Is 30.530:
\[\begin{align*} \hat{\text{BMI}} & = 30.205 + (0.325 \times 1) + (-1.383 \times 0) \\ & = 30.205 + 0.325 + 0 \\ & = 30.530 \end{align*}\]
Interpretting the Effects (cont.)
\[\hat{\text{BMI}} = 30.205 + (0.325 \times \text{Sex}) + (-1.383 \times \text{Feeling Safe})\]
- The predicted BMI for
- A male (0)
- Who does feel safe (1)
- Is 29.147:
\[\begin{align*} \hat{\text{BMI}} & = 30.205 + (0.325 \times 0) + (-1.383 \times 1) \\ & = 30.205 + 0 - 1.383 \\ & = 29.147 \end{align*}\]
- Etc.
The
Flexibility of
Linear Models
Linear Models vs. ANOVAs
- ANOVA (and ANCOVA, MANOVA, etc.)
- Is a type of linear regression
- Results focus on significance of variables
- When all are present in the model together
- Linear Regression
- Is a more flexible framework
- Can model complex relationships & data structures
- E.g., non-linear relationships & nested data
- Can test whole models
- And effects on the whole model when variables are added or removed
Questions Best Addressed by ANOVAs vs. Linear Models
- ANOVAs (and ANCOVAs, MANOVAs, etc.) can ask:
- Which variable is significant?
- Is there an interaction between variables?
- Linear regressions can also ask:
- What is the best combination of variables?
- Does a given variable—or set of variables—significantly contribute to what we already know?
Signal-to-Noise in Linear Models
\(\hat{Y}_{i} = b_{0} + b_{1}X_{i1} + e_{i}\)
- The variance in \(\hat{Y}_{i}\) is
divided into:
- Changes due to the predictors—the “signals”
- Changes due to “other things” (and relegated to error / noise term(s)
- (N.b., the intercept, \(b_{0}\), is a constant when measuring \(\hat{Y}_{i}\), and so not included in this partitioning of the variance in \(\hat{Y}_{i}\))
Signal-to-Noise in Linear Models (cont.)
\(\hat{Y}_{i} = b_{0} + b_{1}X_{i1} + e_{i}\)
- The sum of squares representation of this partition into predictors & error looks like:
\[\sum\limits_{i=1}^{n} (Y_{i} - \overline{Y})^{2} = \sum\limits_{i} (\hat{Y}_{i} - \overline{Y})^{2} + \sum\limits_{i} ({Y}_{i} - \hat{Y}_{i})^{2}\]
Signal-to-Noise in Linear Models (cont.)
\(\sum\limits_{i=1}^{n} (Y_{i} - \overline{Y})^{2} = \sum\limits_{i} (\hat{Y}_{i} - \overline{Y})^{2} + \sum\limits_{i} ({Y}_{i} - \hat{Y}_{i})^{2}\)
- I.e.,the squared sum of the differences of each instance (\(Y_{i}\)) from the mean (\(\overline{Y}\)) equals:
- The squared sum differences of each predicted value (\(\hat{Y}_{i}\)) from the mean
- Plus the squared sums of differences of the actual values (\(Y_{i}\)s) from the respective predicted values
Signal-to-Noise in Linear Models (cont.)
- Another way of saying this:
\(\sum\limits_{i=1}^{n} (Y_{i} - \overline{Y})^{2} = \sum\limits_{i} (\hat{Y}_{i} - \overline{Y})^{2} + \sum\limits_{i} ({Y}_{i} - \hat{Y}_{i})^{2}\)
- Is to say this:
\(\text{Total SS = SS from Regression + SS from Error}\)- Or, further condensed as:
- \(SS_{Total} = SS_{Reg.} + SS_{Error}\)
- Or, further condensed as:
Signal-to-Noise in Linear Models (end)
- Using \(SS_{Total} = SS_{Reg.} +
SS_{Error}\),
- We can compute the ratio of predicted to actual:
Ratio of Predicted-to-Actual Variance = \(\frac{SS_{Reg.}}{SS_{Total}}\)- Or, equivalently as \(1 - \frac{SS_{Reg.}}{SS_{Error}}\)
- We can compute the ratio of predicted to actual:
- We typically represent this ratio as R²:
\[R^{2} = \frac{SS_{Reg.}}{SS_{Total}} = 1 - \frac{SS_{Reg.}}{SS_{Error}}\]
Yep, that’s what \(R^{2}\) means in ANOVAs ☻
Adding More Terms to Models
- Adding another variable to the equation:
\(\hat{Y}_{i} = b_{0} + b_{1}X_{i1} + b_{2}X_{i2} + e_{i}\)- \(X_{i2}\) = Participant \(i\)’s value on the other variable (\(X_{2}\)) added to the model
- \(b_{2}\) = Slope for \(X_{2}\)
- Since there are multiple predictors (\(X\)s) in this model,
- This is called a multiple linear regression
More About the Equation (cont.)
- We can continue to add still more variables to the model, e.g., \(X_{3}\) and \(X_{3}\):
\[\hat{Y}_{i} = b_{0} + b_{1}X_{i1} + b_{2}X_{i2} + b_{3}X_{i3} + b_{4}X_{i4} + e_{i}\]
- When there are a lot of terms in the model, then we usually
abbreviate the equation to:
\[\hat{Y}_{i} = b_{0} + b_{1}X_{i1} ... + b_{k}X_{ik} + e_{i}\]- Were \(k\) denotes the number of variables
Adding More Terms to Models (cont.)
\(\hat{Y}_{i} = b_{0} + b_{1}X_{i1} ... + b_{k}X_{ik} + e_{i}\)
- We can test interactions by adding additional terms
- E.g., \(... b_{1}X_{i1} + b_{2}X_{i2} + \mathbf{b_{3}(X_{i1}X_{i2}}) ...\)
- Or test non-linear effects, also by adding terms
- E.g., \(... b_{1}X_{i1} + \mathbf{b_{2}X_{i1}^{2}} ...\)
Adding More Terms to Models (end)
- Just as we separated out the effects of the predictors,
- We can separate out sources of error
- E.g., per predictor/term in the model
- We can separate out sources of error
- We can also combine error terms
- E.g., we can “nest” one variable into another
- Patients nested within hosptital units
- Wave (time) nested within patient
- E.g., we can “nest” one variable into another
Modeling Linear & Non-Linear Relationships
\(\hat{Y}_{i} = b_{0} + b_{1}X_{i1} ... + b_{k}X_{ik} + e_{i}\)
- \(Y\) is assumed to follow a
certain distribution
- This determines how error is modeled
- E.g., is error usually assumed to be normally distributed
- But both distributions can be assumed to be something else
- E.g., logarithmic
Modeling Linear & Non-Linear Relationships (cont.)
\(\hat{Y}_{i} = b_{0} + b_{1}X_{i1} ... + b_{k}X_{ik} + e_{i}\):
- \(X\)s can be nominal, ordinal,
interval, or ratio
- This affects how those variables are modeled
- As well as the error related to them
- We could transform the terms on the right
- E.g., raise them to a power or take their log
Modeling Linear & Non-Linear Relationships (cont.)
\(\hat{Y}_{i} = b_{0} + b_{1}X_{i1} ... + b_{k}X_{ik} + e_{i}\)
- For an ANOVA (and t-tests):
- \(Y\) is assumed to be normally distributed
- The \(X\)s are nominal
- The model terms are not transformed
- Leaving their relationship with \(Y\) linear
- Technically, called an “identity transformation”
- Meaning they are multiplied by 1:
\(\hat{Y}_{i} = 1 \times (b_{0} + b_{1}X_{i1} ... b_{k}X_{ik} + e_{i})\)
- Meaning they are multiplied by 1:
Modeling Linear & Non-Linear Relationships (end)
- The terms can be transformed in other models
- This transformation is called a Link Function
- Since it “links” the terms on the right to the predicted value of \(Y\) on the left
- This transformation is called a Link Function
- E.g., logistic regression uses a logarithmic (\(e\)) link:
\(\hat{Y}_i = \frac{e^{b_{0} + b_{1}X_{i1} + \cdots + b_{k}X_{ik}}}{1 + e^{b_{0} + b_{1}X_{i1} + \cdots + b_{k}X_{ik}}}\)
which is more often written as:
\(\ln\!\frac{\hat{Y}_i}{1-\hat{Y}_i} = \;b_{0}+b_{1}X_{i1}+\cdots+b_{k}X_{ik}\)
Generalized Linear Models
- That family of models is referred to as generalized
linear models
- I.e., we can generalize that linear model into other types of models
- ANOVAs, t-tests, and logistic regressions are types of generalized linear models
- Generalized linear models typically use maximum
likelihood estimation (MLE) to compute terms
- The ordinary least squares of ANOVAs, etc. is itself a specific type of MLE
Generalized Linear Models (cont.)
- N.b., confusingly, in addition to generalized linear
models,
- There are general linear models
- “General linear model” simply refers to models you
already know.
- I.e., those with:
- Normally-distributed,
iidvariables & - Identity link functions
- Normally-distributed,
- Like ANOVAs & multiple linear regressions
- I.e., those with:
Generalized Linear Models (cont.)
- Assumptions of generalized linear models:
- Relationship between response and predictors must be expressible as
a linear function
- But many can model heteroscedasticity well
- Cases must be independent of each other
- Or that relationship should be part of the model
- Often as nesting
- Or that relationship should be part of the model
- Relationship between response and predictors must be expressible as
a linear function
Generalized Linear Models (end)
- Assumptions of generalized linear models (cont.):
- Predictors should not be too inter-correlated (lack of multicollinearity)
- Linear regression simply cannot get accurate measures of two effects if they cannot be easily separated
- The random error & link functions should approximate their actual functions
- Predictors should not be too inter-correlated (lack of multicollinearity)
Further Considerations
Multicollinearity
- When two or more predictors share a lot of variance
- I.e., are strongly correlated
- E.g., r ≥ .8 (Dormann et al., 2013)
- I.e., are strongly correlated
- Two general sources:
- Structural: Caused by how the model was constructed
- E.g., adding interaction terms
- Data: Caused by variables that are inherently correlated
Multicollinearity (cont.)
- Problems caused by multicollinearity:
- Parameter estimates of multicollinear terms can be unstable
- And can even reverse sign
- Reduces the power of the whole model
- Because the parameter estimates are less precise
- Parameter estimates of multicollinear terms can be unstable
Multicollinearity (cont.)
- Multicollinearity shouldn’t affect the whole model’s R²
- Or the model’s good-of-fit statistics
- It mostly impairs interpretation of individual predictors
- Can be tested with variance inflation factor (VIF)
- VIF ranges from 1 to \(\infty\)
- Where values >10 may indicate problems (e.g., Salmerón et al. 2016)
Multicollinearity (cont.)
- Addressing multicollinearity
- Centering variables (subtracting the mean) can reduce structural multicollinearity (Iacobucci et al., 2016)
- Remove one of the correlated variables
- Only test/compare overall model fit
- Use another analysis
Multicollinearity (end)
- Multicollinearity is typically not a concern if the variables with
high multicollinearity are:
- Control variables
- Intentional products of other variables
- E.g., interaction terms, raised to a power, etc.
- Dummy variables
Independence of Cases
- When one case (participant, round of tests, etc.) is correlated with another case
- Can also produce unstable parameter estimates
- Thus affecting significance tests
- Through both false positives (Type 1) & false negatives (Type 2)
- Thus affecting significance tests
- May also affect model goodness of fit
- And not isolated to a few predictors
Independence of Cases (cont.)
- Addressing non-independence
- Best is through research design
- Can also model inter-dependence
- E.g., nesting cases
- As is done explicitly in multilevel (hierarchical) models
- E.g., nesting cases
The Games
- Space Invaders
- Lunar Lander
- Asteroids (Doesn’t work well on Firefox)
- Tempest
- Star Wars
- Battlezone
- Elite